백야극광: 한붓그리기 알고리즘③ - 플레이어가 다른 타일로 이동하기(2)

</br> 전편에 이어서~~

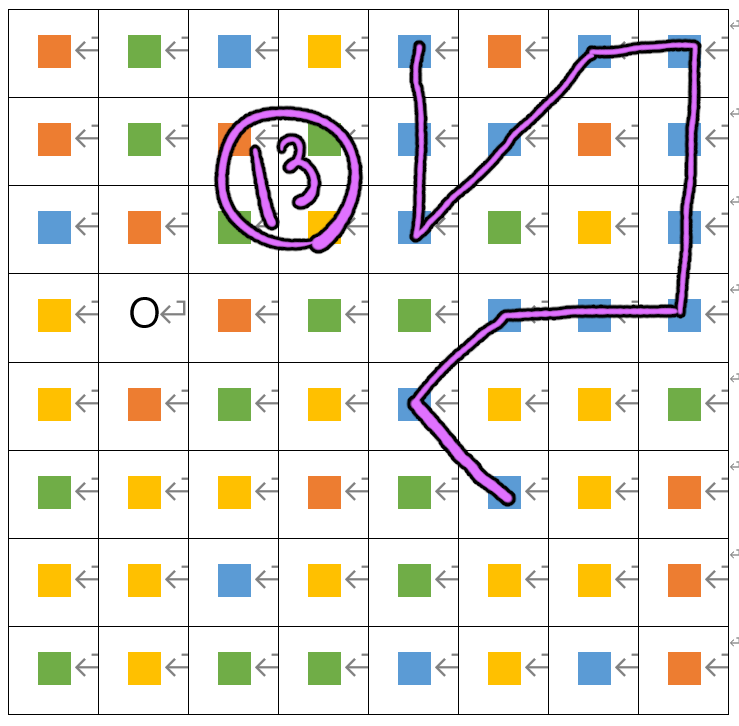
전 편에서, 왼쪽 그림과 같이 맵에서 가장 큰 콤보를 쌓을 수 있는 후보가 될 수 있는 타일들을 찾아냈다.
여기서 가장 긴 콤보를 찾아야 한다. 왜냐하면 그 후에 플레이어가 이동할 타일을 결정할 수 있기 때문이다.

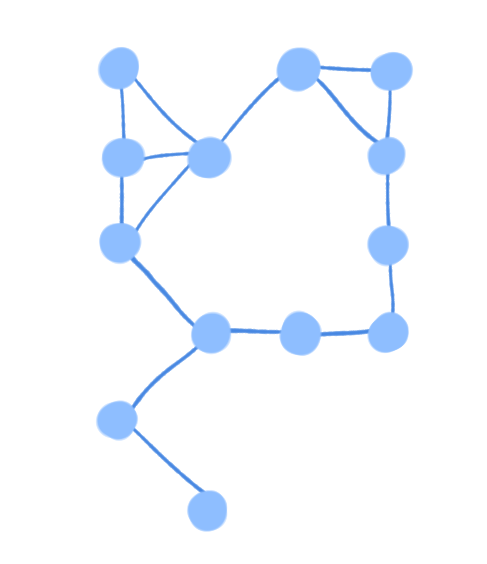
그런데 이는 오른쪽과 같이 그래프로도 볼 수 있다!
따라서 그래프 이론이 도움이 될 것 같다.
</br>

그래프

잠깐 정리하자면…

• trail: 에지가 다 다른 워크
• path: 버텍스가 다 다른 워크
• cycle: 닫힌 패스
• directed / undirected: 유향, 무향

따라서 무향 그래프에서 가장 긴 패스를 찾는 것이 가장 긴 콤보를 찾는 것과 같다고 볼 수 있겠다.
</br>

결론

검색어는 ‘finding longest path in an undirected and unweighted graph’

위키트리에 나와 있다. https://en.wikipedia.org/wiki/Longest_path_problem

In contrast to the shortest path problem, which can be solved in polynomial time in graphs without negative-weight cycles, the longest path problem is NP-hard and the decision version of the problem, which asks whether a path exists of at least some given length, is NP-complete. This means that the decision problem cannot be solved in polynomial time for arbitrary graphs unless P = NP.

즉 NP hard 문제다…

수업 시간에 배우기로 트리의 경우엔 BFS 두 번으로 최장 거리를 알 수 있는데, 그냥 그래프는 할 수 없다. 그냥 다 계산하는 수 밖에…
</br>

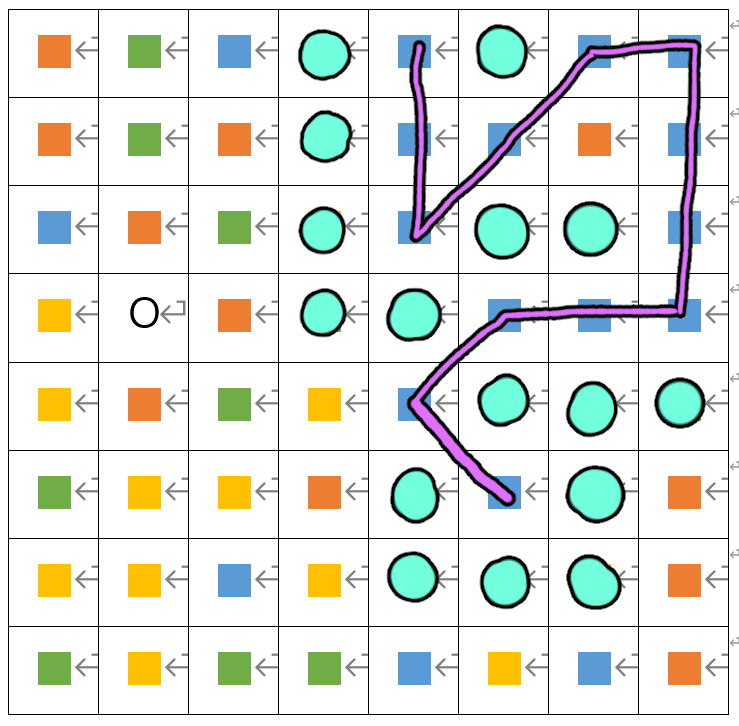
코드는 어차피 거의 비슷한 dfs의 반복이라 생략한다. 모든 타일들에서 dfs를 수행하고, 맥스 콤보를 만들 수 있는 시작점들을 모두 구해 그 주변 8 타일들을 표시한다(플레이어가 이동할 수 있는 곳).

</br>

---

그래프를 패턴을 찾아 단순화해서 트리로 바꿔 볼까, cut vertex를 찾아서 걔네는 빼고 검사해 볼까도 계속 생각해 봤는데, 아무래도 별 성과는 없어서 생략한다ㅜㅜ

지금은 일단 넘어 가자~~
</br>