백야극광: 한붓그리기 알고리즘③ - 플레이어가 다른 타일로 이동하기(1)
</br>
2편에 이어서~~
전 포스트에서 백야극광 전투 시스템 퍼즐의 알고리즘을 간단한 Branch and Bound를 통해 성능을 늘여 보았다.
이번에는 스킬을 추가해 보자. 캐릭터들의 스킬에는
- 무작위로 타일 바꾸기
- 플레이어가 다른 타일로 이동하기
- 타일을 선택해서 원하는 색으로 바꾸기
가 있다. 무작위로 바꾸는 건 제외하고, 뒤의 두 가지는 구현해 보도록 한다.
이번엔 2번, 플레이어가 다른 타일로 이동하기를 만들어 보자~~
</br>
테스트 케이스
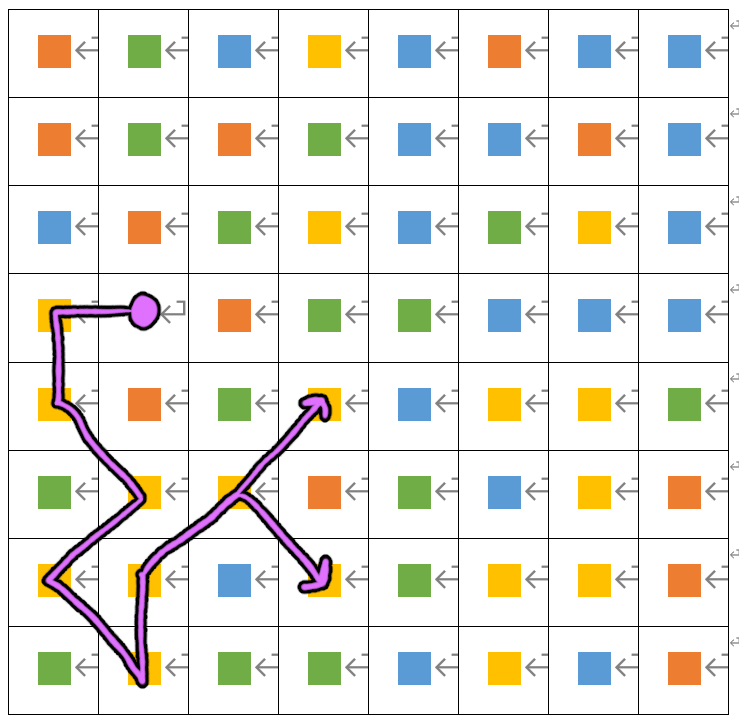
8 X 8 맵을 예시로 보자. 실행 결과 노란색 타일로 갈 경우 콤보가 8로, 가장 크다. 경로는 오른쪽 그림과 같이 두 가지가 있다.
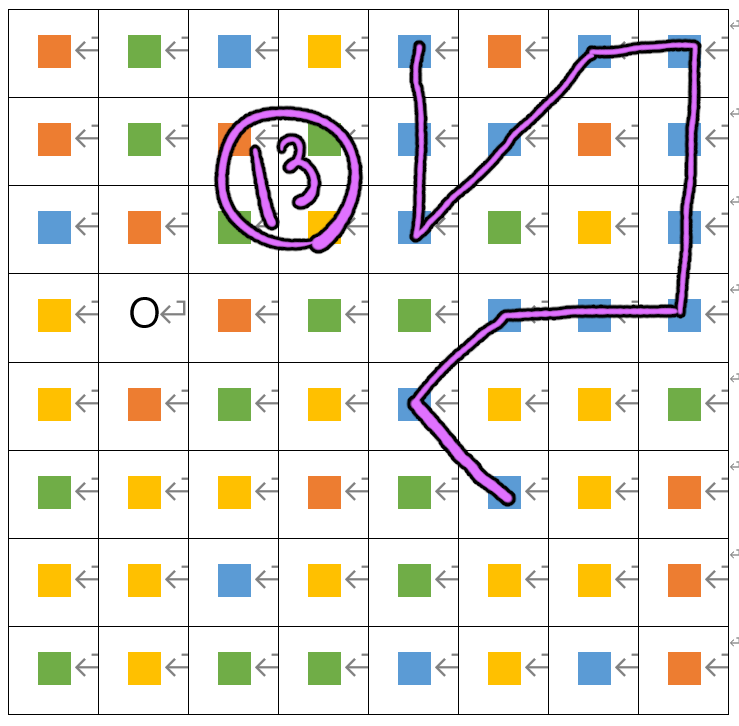
그러나 맵을 잘 보면 파란색 타일들이 13개 콤보를 쌓을 수 있게 배치 되었다.
따라서 플레이어가 청록색으로 표시한 곳으로 이동한다면, 맵 내에서의 최대 콤보를 쌓을 수 있게 된다.
</br>
코드
즉 해야 할 일은 맵에서 다른 가장 긴 콤보가 될 수 있는 타일들을 찾아야 한다.
for(int i = 1; i < N+1; i++){
for(int j = 1; j < N+1; j++){
check[i][j] = 1;
func(i, j, mmap2[i][j], 1);
check[i][j] = 0;
}
}
그런데 이렇게 그냥 맵의 모든 타일들을 for문으로 돌려 dfs를 다 시행하면 수행 시간이 낭비다. 또, 연결된 타일들을 이미 검사했는데 또 검사해야 한다.
따라서 맵을 복사해 보조 기억들을 메모할 mmap2[12][12]를 추가했다. 여기에 이미 탐색한 타일들을 표시해 둔다.
#include <bits/stdc++.h>
#define P tuple<int, int, int>
#define gt(t, a) get<a>(t)
#define mt(a, b, c) make_tuple(a, b, c)
using namespace std;
int N;
char mmap[12][12];
char mmap2[12][12];
int check[12][12];
int checkNum = 1;
int maxCombo; char maxColor;
map<char, int> colors;
set<P> kids;
int moveI[8] = { -1, -1, -1, 0, 1, 1, 1, 0 };
int moveJ[8] = { -1, 0, 1, 1, 1, 0, -1, -1 };
/*
1 2 3
8 O 4
7 6 5
*/
struct cmp{
bool operator()(P p1, P p2){
return gt(p1, 2) < gt(p2, 2);
}
};
struct cmps{
bool operator()(set< P > s1, set< P > s2){
return s1.size() < s2.size();
}
};
void func(int x, int y, char c, int d){
if( d > maxCombo ){
maxCombo = d;
maxColor = c;
}
// cout << x << ' ' << y << ' ' << c << ' ' << d << endl;
for(int i = 0; i < 8; i++){
int nextX = x + moveI[i];
int nextY = y + moveJ[i];
if( check[nextX][nextY] == 0 && mmap[nextX][nextY] == c ){
check[nextX][nextY] = 1;
if(mmap2[nextX][nextY] != 'O'){
mmap2[nextX][nextY] = 'O';
checkNum++;
}
func(nextX, nextY, c, d+1);
check[nextX][nextY] = 0;
}
}
}
void func2(int x, int y, char c, int d){
// cout << x << ' ' << y << ' ' << c << ' ' << d << endl;
for(int i = 0; i < 8; i++){
int nextX = x + moveI[i];
int nextY = y + moveJ[i];
if( check[nextX][nextY] == 0 && mmap2[nextX][nextY] == c ){
check[nextX][nextY] = 1;
kids.insert(mt(nextX, nextY, c));
func2(nextX, nextY, c, d+1);
check[nextX][nextY] = 0;
}
}
}
int main(){
ifstream inp;
inp.open("2.inp");
ofstream out;
out.open("2.out");
colors.insert(pair<char, int>('R', 0));
colors.insert(pair<char, int>('G', 0));
colors.insert(pair<char, int>('B', 0));
colors.insert(pair<char, int>('Y', 0));
colors.insert(pair<char, int>('O', 0));
inp >> N;
for(int i = 0; i < N+2; i++)
mmap[i][0] = '\u0000';
for(int i = 0; i < N+2; i++)
mmap[0][i] = '\u0000';
for(int i = 0; i < N+2; i++)
for(int j = 0; j < N+2; j++)
check[i][j] = 0;
int startI, startJ;
for(int i = 0; i < N; i++){
string s;
inp >> s;
for(int j = 0; j < N; j++){
mmap[i+1][j+1] = s[j];
mmap2[i+1][j+1] = s[j];
colors[s[j]]++;
if( s[j] == 'O' ){
startI = i+1;
startJ = j+1;
}
}
}
inp.close();
priority_queue< P, vector<P>, cmp > pq;
for(int i = 0; i < 8; i++){
int x = startI + moveI[i];
int y = startJ + moveJ[i];
int c = colors[mmap[x][y]];
P p = P(x, y, c);
pq.push(p);
}
while( pq.size() ){
cout << "----------------------START" << endl;
P p = pq.top();
if( gt(p, 2) >= maxCombo ){
check[gt(p, 0)][gt(p, 1)] = 1;
func(gt(p, 0), gt(p, 1), mmap[gt(p, 0)][gt(p, 1)], 1);
if( mmap2[gt(p, 0)][gt(p, 1)] != 'O' ){
mmap2[gt(p, 0)][gt(p, 1)] = 'O';
checkNum++;
}
}
check[gt(p, 0)][gt(p, 1)] = 0;
pq.pop();
}
priority_queue< P, vector< set<P> >, cmps > pqs;
for(int i = 1; i < N+1; i++){
for(int j = 1; j < N+1; j++){
if( mmap2[i][j] != 'O' ){
check[i][j] = 1;
kids.insert(mt(i, j, mmap2[i][j]));
func2(i, j, mmap2[i][j], 1);
checkNum += kids.size();
if( kids.size() > maxCombo ) pqs.push(kids);
for(auto it = kids.begin(); it != kids.end(); it++){
P p = *it;
mmap2[gt(p, 0)][gt(p, 1)] = 'O';
}
kids.clear();
check[i][j] = 0;
}
if( checkNum > N * N - maxCombo ) break;
}
}
while( pqs.size() ){
set<P> s = pqs.top();
if( s.size() > maxCombo ){
for(auto it = s.begin(); it != s.end(); it++){
P p = *it;
// cout<<gt(p, 0)<< ' '<<gt(p, 1)<<endl;
}
// cout<<endl<<endl;
pqs.pop();
}
else{
pqs = priority_queue< P, vector< set<P> >, cmps >();
}
}
out << maxColor << ' ' << maxCombo << endl;
out.close();
}
전체 코드다.
기존의 플레이어의 위치에서 가장 큰 콤보를 찾는 코드는 거의 동일하지만, func() 함수에서 이미 탐색한 타일들을 표시하는 코드를 추가했다.
priority_queue< P, vector< set<P> >, cmps > pqs;
for(int i = 1; i < N+1; i++){
for(int j = 1; j < N+1; j++){
if( mmap2[i][j] != 'O' ){
check[i][j] = 1;
kids.insert(mt(i, j, mmap2[i][j]));
func2(i, j, mmap2[i][j], 1);
checkNum += kids.size();
if( kids.size() > maxCombo ) pqs.push(kids);
for(auto it = kids.begin(); it != kids.end(); it++){
P p = *it;
mmap2[gt(p, 0)][gt(p, 1)] = 'O';
}
kids.clear();
check[i][j] = 0;
}
if( checkNum > N * N - maxCombo ) break;
}
}
전체 맵에서 현재 최대 콤보보다 큰, 가장 큰 콤보가 될 수 있는 부분들을 찾는 for문이다.
계산 횟수를 줄이기 위해서, mmap2[][]에서 이미 방문한 타일이 아닐 경우 dfs를 수행한다.
set<P> kids에 현재 dfs에서 방문한 타일들을 저장한다. 만약 kids의 크기가 현재 최대 콤보 보다 크다면 맵에서 새로운 더 큰 콤보를 만들 수 있는 타일들일 수 있으므로 우선순위 큐 pqs에 저장한다.
또, 만약 현재 확인한 타일들의 수가 맵 전체 타일 수에서 현재 최대 콤보를 뺀 것보다 크다면, 아직 확인 안 한 타일들의 총 개수가 현재 최대 콤보보다 더 작으므로 이들을 검사할 필요는 없다. 따라서 for문을 종료한다.
struct cmps{
bool operator()(set< P > s1, set< P > s2){
return s1.size() < s2.size();
}
};
// in main()
while( pqs.size() ){
set<P> s = pqs.top();
if( s.size() > maxCombo ){
for(auto it = s.begin(); it != s.end(); it++){
P p = *it;
// cout<<gt(p, 0)<< ' '<<gt(p, 1)<<endl;
}
// cout<<endl<<endl;
pqs.pop();
}
else{
pqs = priority_queue< P, vector< set<P> >, cmps >();
}
}
따라서 우선순위 큐 pqs에는 맵의 플레이어가 갈 수 없는 곳에서, 최대 콤보를 만들 가능성이 있는 셋들이 크기 순으로 들어가 있다.
</br>
출력 결과
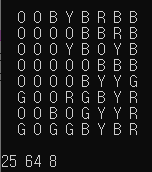
플레이어가 갈 수 있는 8개의 타일들을 모두 탐색하고 난 후의 mmap2가 출력된 상태다.
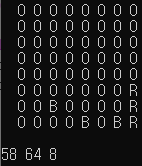
아직 탐색되지 않은 타일들의 수가 플레이어가 찾은 최대 콤보의 수보다 작으므로 for문이 종료될 때의 출력이다.

플레이어가 찾은 최대 콤보보다 연결된 타일들의 수가 더 큰 set의 출력이다.
</br>
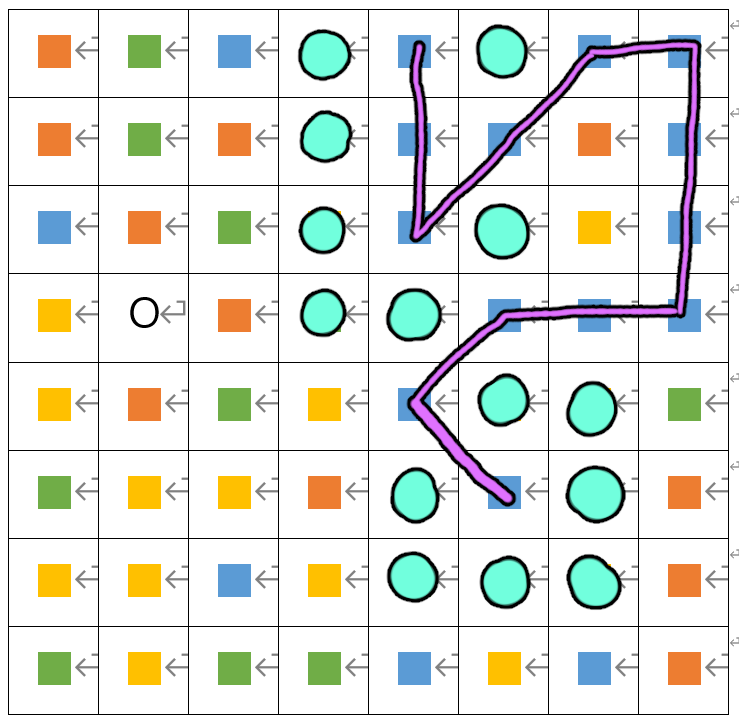
자~ 이제 맵에서 더 큰 콤보를 쌓을 수 있을 후보들은 찾았다.


다시 이 사진들을 보면… 파란색 타일들의 좌표는 다 알았는데, 최대 콤보 수는 아직 알 수 없는 상황이다.
타일 개수는 13개지만 최대 콤보가 13이라는 보장이 없기 때문이다. 예를 들어 (3, 8)과 같이 연결된 중간에서 시작하면 다른 타일들에 갈 수도 없고…
그래서 플레이어가 이동할 타일, 즉 청록색으로 표시한 타일들을 다 찾아 내려면 set의 타일들에서 다 dfs로 찾아 봐야 하나? 좀 많이 걸리지 않나? 해서 관련 알고리즘을 찾아 보는 중이다.
다음 편에!!!
</br>
댓글남기기