백준: 타일 채우기, 타일링 ②(14852, 11333, 2718)

타일링 이어서

14852: 타일 채우기 3

https://www.acmicpc.net/problem/14852

문제: 2*N 크기 벽을 2*1, 1*2, 1*1 타일로 채우는 경우의 수

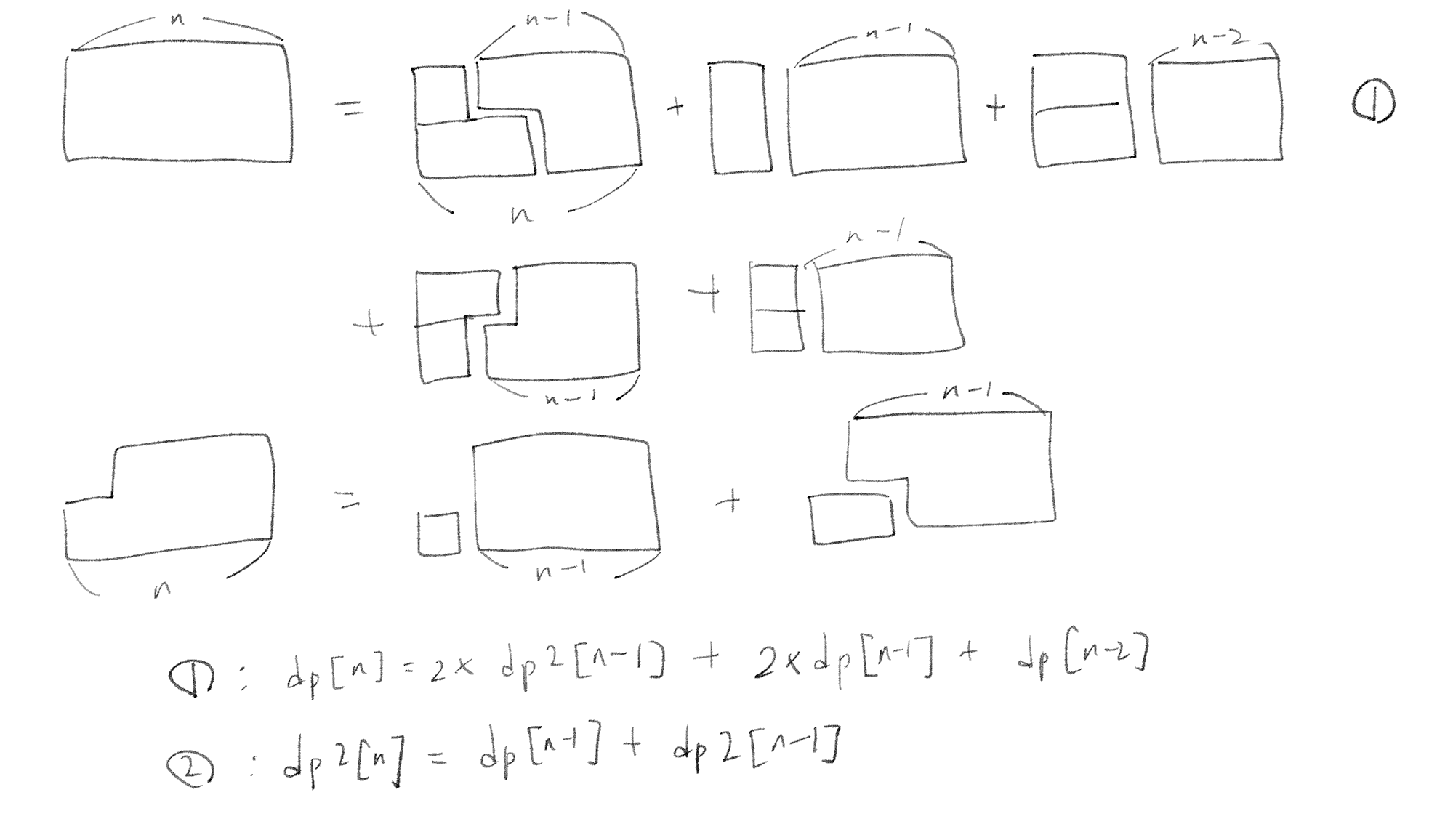
이번엔 1*1 타일이 추가 되었다.
적당히 나눠 주면 된다

1번 경우에서 처음에 이런 식으로 나눴더니, 겹치는 경우가 막 생겨서 상당히 곤란했다

#include <bits/stdc++.h>
#define MOD 1000000007

using namespace std;

long long dp[1000001];
long long dp2[1000001];

int main(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);

    int n;
    cin >> n;

    dp[0] = 1;
    dp[1] = 2;
    dp2[1] = 1;
    for(int i = 2; i <= n; i++){
        dp[i] = 2l * dp2[i-1] + 2l * dp[i-1] + dp[i-2];
        dp2[i] = dp[i-1] + dp2[i-1];
        dp[i] = dp[i] % MOD;
        dp2[i] = dp2[i] % MOD;
    }

    cout << dp[n] << endl;

}

이 문제는 모듈러 해주는 걸 잊으면 안 된다

dp[i] = (((2 * dp2[i-1]) % MOD + (2 * dp[i-1]) % MOD) % MOD + dp[i-2]) % MOD;
dp2[i] = (dp[i-1] + dp2[i-1]) % MOD;

long long 타입을 안 쓰고 int로 배열을 선언해서 MOD를 자주 해주는 방식으로도 한 번 제출해 봤다

시간은 별 차이 없고 메모리는 확실히 줄어든다.

11333: 4×n 타일링

https://www.acmicpc.net/problem/11333

문제: 4*N 크기 벽을 3*1, 1*3 타일로 채우는 경우의 수

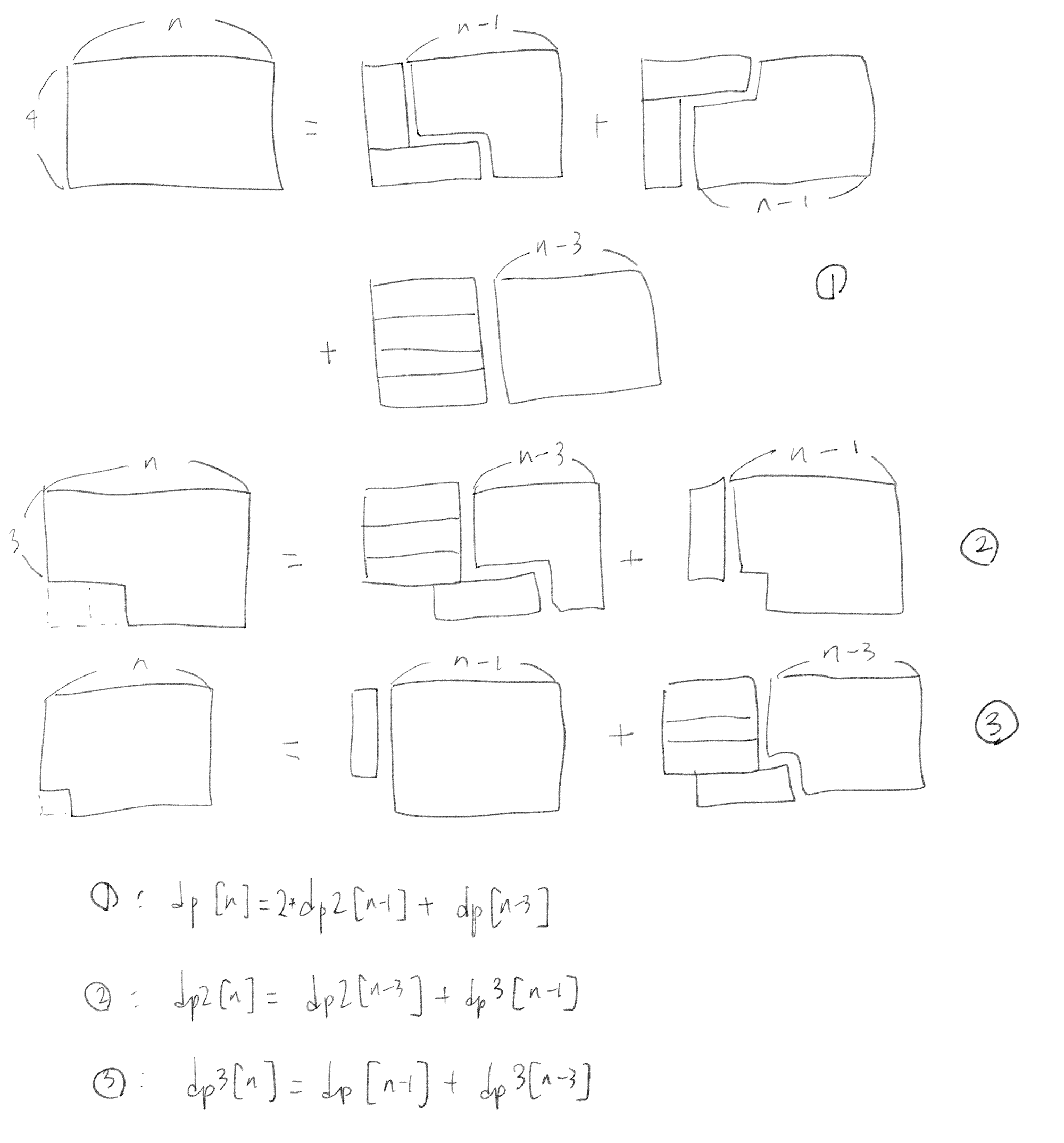
얘도 적당히 안 겹치게 잘 짠다. 근데 짜다 보니까 점화식이 3개나 필요하게 됐다.
다른 애들은 골드 5고 얘는 골드 2던데 그래서 그런 건지?? 아니면 줄일 수 있을랑가

#include <bits/stdc++.h>
#define MOD 1000000007

using namespace std;

long long dp[10001];
long long dp2[10001];
long long dp3[10001];

int main(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);

    int t;
    cin >> t;

    dp[0] = 1;
    dp[3] = 3;
    dp2[2] = 1;
    dp3[1] = 1;
    for(int i = 3; i <= 10000; i++){
        dp[i] = 2 * dp2[i-1] + dp[i-3];
        dp2[i] = dp2[i-3] + dp3[i-1];
        dp3[i] = dp[i-1] + dp3[i-3];
        dp[i] = dp[i] % MOD;
        dp2[i] = dp2[i] % MOD;
        dp3[i] = dp3[i] % MOD;
    }

    while( t-- ){
        int n;
        cin >> n;
        cout << dp[n] << '\n';
    }

}

얘도 뭐 모듈러 잘 해주고 여러 개 받아서 출력하면 끝

2718: 타일 채우기

https://www.acmicpc.net/problem/2718

문제: 4*N 크기 벽을 2*1, 1*2 타일로 채우는 경우의 수

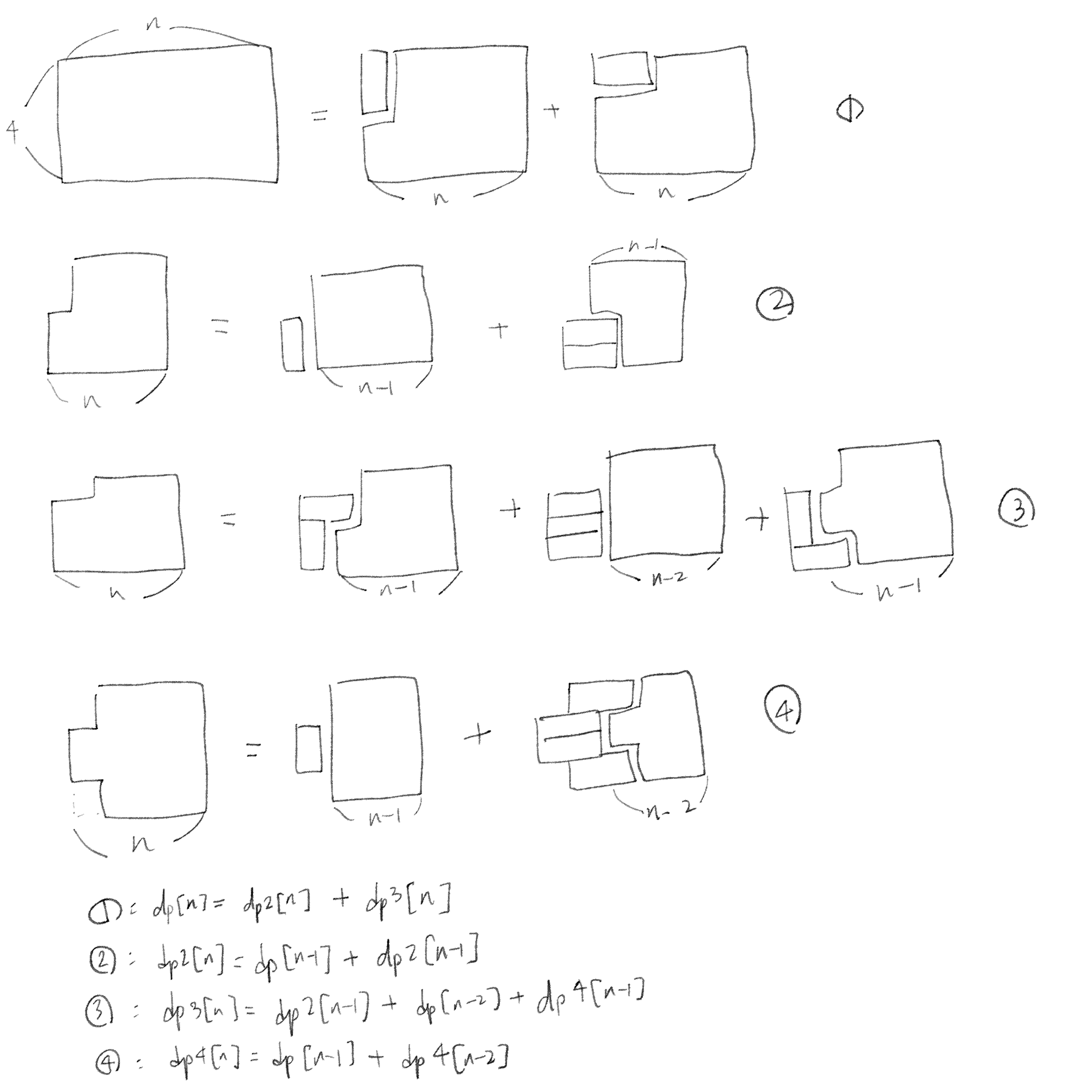
식이 4개 나온다 얘는 골드 1이다ㅋㅋ 이거 맞는 건가
그래도 식 자체는 간단한 편

#include <bits/stdc++.h>

using namespace std;

int dp[27];
int dp2[27];
int dp3[27];
int dp4[27];

int main(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);

    int t;
    cin >> t;

    dp[0] = 1; dp[1] = 1; dp[2] = 5;
    dp2[0] = 1; dp2[1] = 1; dp2[2] = 2;
    dp3[0] = 1; dp3[1] = 0; dp3[2] = 2;
    dp4[0] = 1; dp4[1] = 1; dp4[2] = 1;
    for(int i = 3; i <= 26; i++){
        dp4[i] = dp[i-1] + dp4[i-2];
        dp3[i] = dp2[i-1] + dp[i-2] + dp4[i-1];
        dp2[i] = dp[i-1] + dp2[i-1];
        dp[i]  = dp2[i] + dp3[i];
    }

    while( t-- ){
        int n;
        cin >> n;
        cout << dp[n] << '\n';
    }

}

정확한 N은 말해주지 않지만 Int 범위 내에서 문제가 나온다는데, N이 대략 24? 25일 때쯤에 오버플로우나더라

---

좋다