백준: 타일 채우기, 타일링 ①(2133, 1720)

오랜만에 문제 풀이다
중간고사 때부터 종강하고 지금까지 쉬었다가 이제 다시 시작한다

타일 문제들은 거의 비슷하다 그림만 잘 그리면 된다 그게 좀 어렵긴 하지만…

기본적인 경우(2*N)

2*N 크기 벽을 2*1, 1*2, 2*2 타일로 채우는 경우의 수를 보자

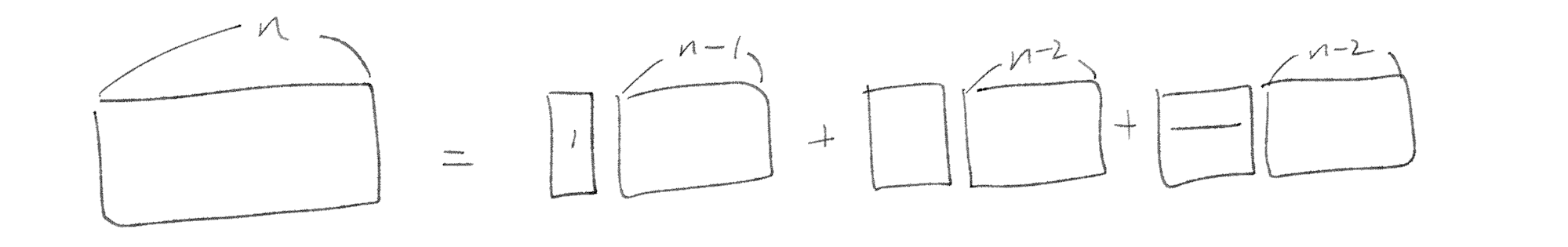
대충 이런 그림이 될 거다
2*1 타일에 2*(n-1)을 붙이거나, 2*2 타일에 2*(n-2)을 붙이거나, 1*2 + 1*2 타일에 2*(n-2)을 붙이는 경우다.

이 때 겹치지 않게 경우를 나누는 게 중요하다.

AB ***
AB ***

예를 들어 위 경우는 1번 경우와 겹쳐지기 때문에 추가하면 안 된다.

dp 식으로 표현하면

dp[n] = dp[n-1] + 2 * dp[n-2];

이 된다.

2133: 타일 채우기

https://www.acmicpc.net/problem/2133

문제: 3*N 크기 벽을 2*1, 1*2 타일로 채우는 경우의 수

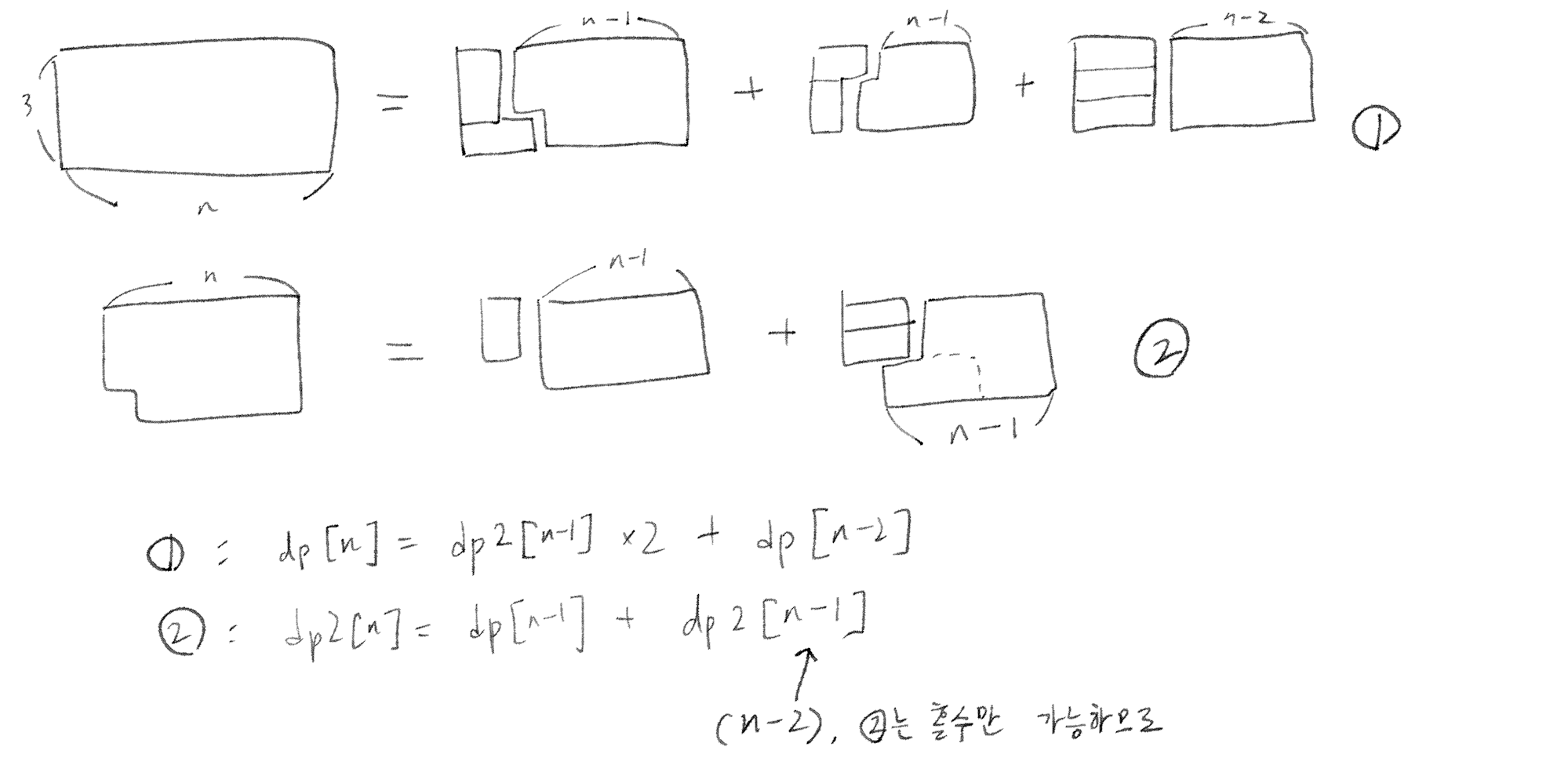
1번 경우와 2번 경우로 나눌 수 있다
물론 이 때도 겹치지 않게 경우를 나누도록 조심해야 한다. 1번에서 나눠가지고 2번으로 가보니 똑같은 경우가 있다던가 하면 안 된다

2번은 그림을 보면 알겠지만 총 칸의 수가 2 + 3*(n-1)이기 때문에 n이 홀수일 때만 가능하고 짝수일 땐 경우의 수가 0이 된다(총 칸의 수가 짝수가 아니므로).
따라서 점화식도 dp2[n-1]을 dp2[n-2]로 적었다. 어차피 똑같음

#include <bits/stdc++.h>

using namespace std;

int dp[31];
int dp2[31];

int main(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);

    int n;
    cin >> n;

    if( n % 2 ){
        cout << 0 << endl;
        return 0;
    }

    dp[2] = 3;
    dp2[1] = 1;
    dp2[3] = 4;
    for(int i = 4; i <= n; i++){
        dp2[i-1] = dp[i-2] + dp2[i-3];
        dp[i] = dp2[i-1] * 2 + dp[i-2];
    }

    cout << dp[n] << endl;

}

식은 뭐 걍 그대로 짜면 됨

1720: 타일 코드

https://www.acmicpc.net/problem/1720

문제: 2*N 크기 벽을 2*1, 1*2, 2*2 타일로 채우는데, 좌우 대칭인 경우 뺀 경우의 수

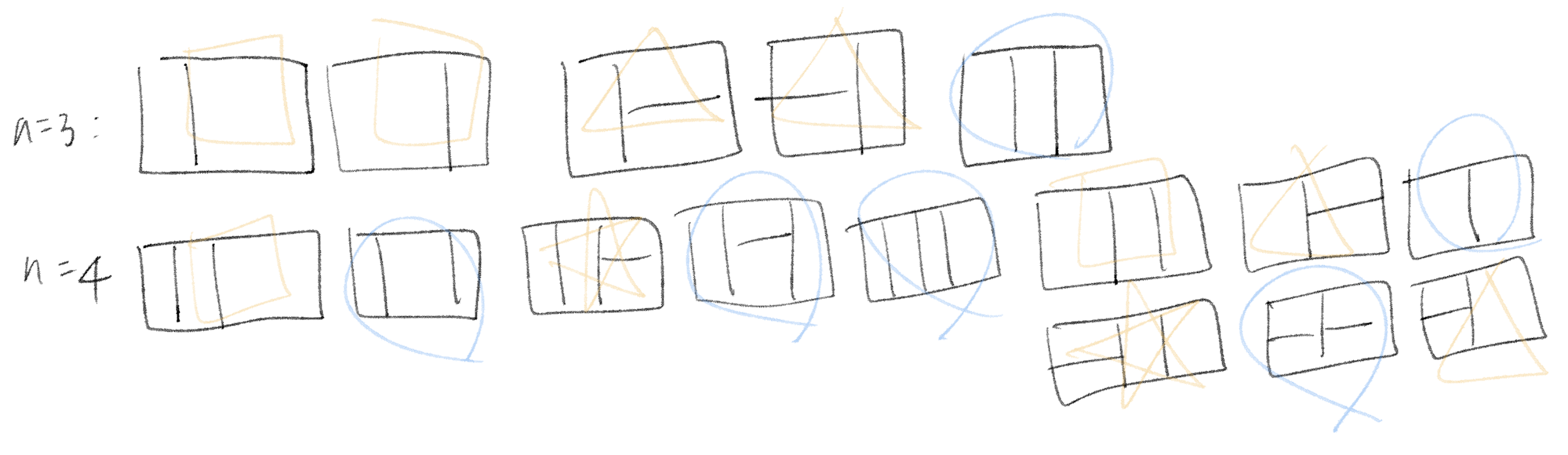
맨 처음 보았던 기본적인 경우에서 좌우 대칭인 것들을 생각해 보자
파란색 동그라미는 좌우 대칭되는 다른 짝이 없는 거고, 각 주황색 도형들은 좌우 대칭되는 짝들이다.

이렇게 보니 그 타일링 자체가 좌우 대칭이면 다른 짝이 없고, 그게 아니면 다 짝이 있게 된다. 생각해 보면 당연함

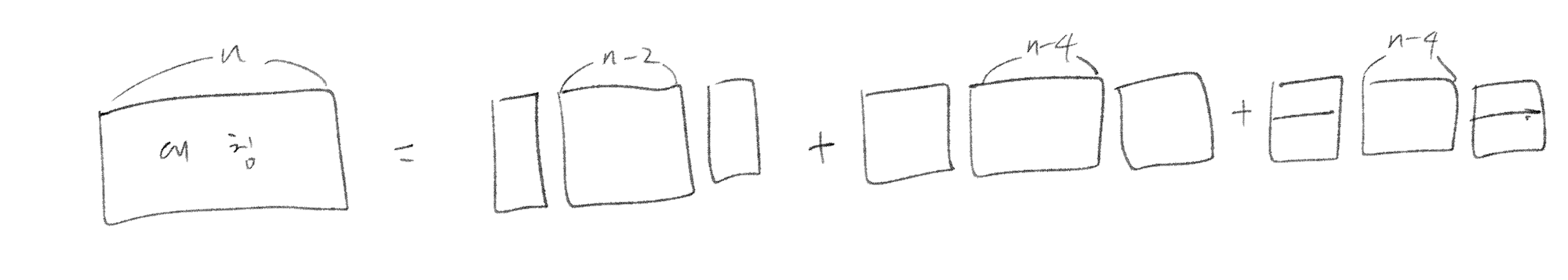
해서 타일링 자체가 좌우 대칭이 되는 경우를 세어 보자
양 옆에 2*1 타일이 붙은 경우나, 2*2 타일이 붙은 경우나, 1*2 + 1*2 타일이 붙은 경우가 있다.

따라서 기존 dp에는 타일링 자체가 좌우대칭인 것들과 좌우대칭이 되는 짝들이 섞여 있으므로,

(좌우대칭이 되는 짝들) = dp[n] - (타일링 자체가 좌우대칭인 것들)

ans = (좌우대칭이 되는 짝들) / 2 + (타일링 자체가 좌우대칭인 것들)

로 구하면 될 거 같다.

    dp[1] = 1;
    dp[2] = 3;
    for(int i = 3; i <= n; i++){
        dp[i] = dp[i-1] + dp[i-2] * 2;
    }

    dp2[0] = 1;
    dp2[1] = 1;
    dp2[2] = 3;
    dp2[3] = 1;
    for(int i = 4; i <= n; i++){
        dp2[i] = dp2[i-2] + dp2[i-4] * 2;
    }

    cout << (dp[n] - dp2[n]) / 2 + dp2[n] << endl;

코드도 뭐 그대로…
베이스 케이스가 0에서 1이 되어야 한다.
만약 0이 될 경우 이전 단계에서 딱 맞게 떨어져서 0으로 넘어 왔을 때의 경우를 체크하지 못하게 된다.

---

길어서 잘라서 올려야 겠넹